まず誤解を解いておきたいんです。

「数学は答えが決まっていてつまらない」っていう意見（アマの目第12回）がありました。 これは多くの人の共通認識かもしれません。 でもこれは偏見で、数学ほど創造性や芸術性が重要である学問はないと私は思います。

答えがひとつに決まっているというのは、そうなるように構成された問題だけを解いてきたに過ぎません。 また仮に答えはひとつであっても、答えに到達するまでの過程は幾通りも存在することが多いです。 そして難問に挑む際に必要な創造性というのは、他の学問よりもはるかに重要です。

確かに、数学は論理だった思考が重要です。論理的に考える能力がないと問題を解くことはできませんが、それだけでは不十分。 解くための「ひらめき」が重要です。「ひらめき」＝創造性というわけです。 それを育成するために、多くの計算問題を解いて引き出しを増やすわけですね。

ちなみに、「ひらめき」が先にきて論理があとでついてくるというようなことも数学ではあります。 有名なところでは「フェルマーの最終定理」がそうでしょう。 17世紀にフェルマーが

3 以上の自然数 n について、xⁿ + yⁿ = zⁿ となる 0 でない自然数 (x, y, z) の組み合わせがない

他にも、インドの魔術師と呼ばれる天才数学者ラマヌジャンなんかもこの部類でしょう。 彼は円周率πに関して以下のような公式を思いつきました（証明なしに）。

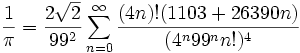
そしてこの公式を思いついた理由を、 「女神が私のベロの上に書いて下さるのです。朝起きたときに書き写すのです。」と言っているのです。 ちなみに彼は32年の生涯で3254個もの公式を遺しています。

ね、数学って創造性が重要だと思いませんか？

…で結局何がいいたかったかというと。

「答えが決まっていてつまらない」っていうのは何も数学に限ったことじゃないと思うんです。

音楽だって、「答えが決まっていてつまらない」演奏ってあるじゃないですか。 馴れ合いで演奏していて先が見えているようなもの。 過去の録音にとらわれてそれを目指すだけの演奏（いわゆる「テープ病」）。 指揮者がゴールを決め付け、それに囚われているような演奏。 CDで音楽を聴くだけではなくライブにいくのは、こういった勝負感を味わいに行くからではありませんか？ アイドルグループの口パクのステージなんて観に行ったってしょうがないわけです。 あれは目的が違うんでしょうけど。

ポルタビアンカが目指しているのはそんな音楽ではありません。 指導者は決してゴールをみせません。演奏者の自主性を求めます。 演奏者と指揮者とが常に勝負しているような、そういう演奏を理想としています。 いまはまだ演奏者のほうが未熟で指導者に引っ張られているのが現状ですが。

そういう考え方ですから、日々の練習と本番とが全く違うということもよくあります。何回冷や汗をかいたか('A`)

そんなポルタビアンカで求められることは、技術的なものよりも感情面のものが多いです。 生活のなかで感じる喜びとか悲しみといった感情の引き出し、そしてそれを演奏として体現するための技術、それを日々の研鑽で身につけていく必要があります。

こうやって考えてみると、数学と音楽って似ていると思いませんか？ 実際、中世ヨーロッパでは、音楽は数学的な学問の一つとして数えられていたようです。 さらに、子供に音楽の練習をさせると数学の成績が伸びたという報告（Rauscher他, 1997）もあるようで大変興味深いです （Wikipedia参照）。

そんなポルタビアンカの練習に触れてみませんか。ワークショップで皆さんの参加をお待ちしています。あ、練習中に方程式を解いたりはしませんからご安心を…。